동시성 (동시성, Concurrency )은 컴퓨터 과학 에서 시간으로 중복 실행되는 계산 을 수반하는 시스템의 특성이며, 이러한 계산은 자원을 공유 할 수있다. 에드가 다이크 스트라 에 따르면, "두 개 이상의 실행 흐름이 동시 병행 될 때 동시성이 나온다"고했다. 공유 자원의 동시 사용에 따라 다양한 문제가 발생한다. 공유 자원에 관한경쟁 상태 는 예측할 수없는 시스템 상태를 발생시킨다. 상호 배제 의 도입으로 경쟁 상태는 막을 수 있지만 교착 상태 나 리소스 부족을 등의 문제가 새롭게 발생한다. 병렬 시스템의 설계에서는 응답 시간을 최소화하고 처리량을 최대화하기 위해, 데이터 교환, 메모리 할당, 실행 일정 등에 관련된 기술의 신뢰성을 추구한다.
목차[ 숨기기 ] |
이론 [ 편집 ]
동시성 이론은 1960 년대 에 칼 아담 페트리 가 독창적 인 페트리 연구를 실시한 이래, 이론적 컴퓨터 과학 의 주요 연구 영역이다. 이후 병렬 시스템을 이해하기위한 다양한 이론 모델, 논리 도구가 개발되어왔다.
모델 [ 편집 ]
모델 개발과 병행 시스템의 이해를위한 형식 방법에는 여러 가지가 개발되어왔다. 다음에 중요한 것은 열거한다.
이러한 동시성 모델의 일부는 먼저 추론과 사양 기술을 목적으로하고있다. 한편, 다른 모델은 전체 개발주기 (병행 시스템의 설계, 구현, 시험, 테스트, 시뮬레이션)을 지원하는 것을 목적으로하고있다.
논리 [ 편집 ]
다양한 때 상 논리 가 동시에 시스템의 이해를 돕기 위해 사용된다. 특히 선형시 상 논리 와 계산 나무 논리 는 동시에 시스템의 각 시점의 상태를 확인하는 데 사용 가능하다. Action Computational Tree Logic과 Hennesy-Miller Logic, 레슬리 란뽀토 의 Temporal Logic of Actions 등은 "액션 (상태 변화)"의 순서를 확인할 수있다. 이러한 논리의 주된 용도는 병렬 시스템의 사양을 설명하기위한 것이다.
실제 병렬 처리 [ 편집 ]
병렬 프로그래밍 은 병렬 시스템을 구현하는 데 사용되는 프로그래밍 언어와 알고리즘으로 구성된다. 일반적으로 병렬 프로그래밍은 병렬 프로그래밍 보다 범위가 넓은으로 다양한 형태의 통신 및 상호 작용에 관계한다. 반면 일반 병렬 시스템은 미리 정해진 갖춘 구성의 통신 패턴을 갖추고있다. 병렬 프로그래밍의 기본 목표는 " 정당성 ","성능 ","견고 "이 포함된다. 운영 체제와 같은 병렬 시스템은 반영구적으로 동작하는 것이 요구되고있다. 일부 병행 시스템은 투명 동시성을 갖게 구현되어있다. 그 경우, 병렬로 작동하는 계산 주체 군은 공유 자원을 사용하지만, 프로그래머는 그 구현은 숨겨져있다.
병렬 시스템은 공유 자원을 사용하기 때문에 공유 리소스에 대한 액세스를 제어하기위한 일종의 조정 을 할 것 (일반적으로 하드웨어)를 구현할 필요가있다. 따라서 무제한 비결정 가 도입 된 병렬 시스템의 정당성과 성능에 영향을 준다.
관련 항목 [ 편집 ]
외부 링크 [ 편집 ]
| ||||||||||||||||||||||||||||||||
식사하는 철학자 문제 ( Dining Philosophers Problem )는 병렬 처리 문제를 일반화 한 예이다. 고전적인 멀티 프로세스 의 동기화 ( 배타 제어 ) 문제이며, 대학 수준의 컴퓨터 과학 과정은 거의 확실 포함되어있다.
1965 년 , 에드가 다이크 스트라 는 5 대의 컴퓨터가 5 개의 테이프 장치에 충돌 액세스하는 동기화 문제를 제시했다. 곧이 문제는 안토니 호아 에서 "식사하는 철학자 문제"변형 말해지는되었다 [1] [2] [3] .
목차[ 숨기기 ] |
문제 [ 편집 ]
5 명의 철학자가 식사하거나 걱정거리를하고있다. 그들의 전에 중간에 스파게티가 들어간 큰 공이 놓인 둥근 식탁이있다. 그 식탁에 5 개의 접시가 놓여져 접시와 접시 사이에 포크가 1 개씩 놓여있다.
최근에는 식기를 " 포크 "가 아닌" 젓가락 "으로 소개하는 사례가 늘고있다 [4] . 젓가락이라면, "한 사람이 2 개 확보해야 식사를 할 수 없다"는 제한이 자연이다. 또한 구미 지역에 젓가락 문화가 인정되어 온 것의 표현이기도 것이다. 본고에서는 이전 형식 채 스파게티를 2 개의 포크로 먹기, 한 설정을 그대로 설명한다.
스파게티를 볼에서 가지고 자신의 접시가 될듯에는 2 개의 포크를 필요로하고 철학자는 한 번에 한 개의 포크 밖에 테이블에서 취할 수 없다. (좌우의 손에서 동시에 양쪽에있는 두 개의 포크를 취할 수 없다는 의미. 먼저 양쪽의 포크를 가지고 다음에 반대 측의 포크를 가지고 간다.) 철학자 끼리는 결코 대화를 하지 않는다. 따라서 5 명이 왼쪽 포크를 집어 오른쪽 포크가 식탁에 놓인 것을 기다린다는 위험한 교착 상태가 발생할 가능성이있다.
문제는 어떻게 행동 규율을 설정하면 ( 동시성 알고리즘 ) 각 철학자가 굶어 않아도 하나, 즉 식사와 사색을 영원히 계속 되나이다.
해설 [ 편집 ]
본래 교착 상태 문제 해설 수단으로 사용되었다. 이 시스템이 교착 상태에 이르기는 "채워지지 않은 요구의 원환"가 존재하는 경우이다. 예를 들면, 철학자 P 1 이 철학자 P 2 의 손에있는 포크를 기다리고, P 2 는 철학자 P 3 것을 ...... 등등 원 환형 요청이 연쇄한다.
예를 들어 각각의 철학자가 다음과 같이 행동한다.
- 왼쪽 포크를 얻을 때까지 사색하고 기다리고 포크를 다룬다.
- 오른쪽 포크를 얻을 때까지 사색하고 기다리고 포크를 다룬다.
- 식사.
- 오른쪽 포크를 둔다.
- 왼쪽 포크를 둔다.
- 먼저 돌아 반복.
이 해법은 잘못되었습니다. 이 방식으로는 교착 상태가 발생, 전 철학자가 왼쪽 포크가 오른쪽 포크를 갖게되는 것을 기다리는 상황이 발생할 수있는 (이 경우 오른쪽 포크는 결코 얻을 수 없다) [ 5] .
시점에 따라 한 철학자가 두 포크를 잡히지 않는 상황이 교착 상태와는 별도로 발생한다. 이 자원 부족을 칭하는 (스타베숀은 "기아"이며,이 용어도 "식사하는 철학자 문제"의 비유에 부수 한 농담이 기원이다). 예를 들어 하나의 포크를 잡은 상태에서 다른 포크를 5 분 정도 기다린 후 일단 포크를두고 5 분 정도 기다린 후 다시 식사를 시도하는 규칙을 설정한다. 이 방법은 교착 상태 해결되는 (시스템은 다른 상태로 변화 해 나가는)가 라이브 락 상태는 피할 수 없다. 만약 5 명의 철학자가 정확히 동시에 식탁에 도착했다면, 일제히 왼쪽 포크를 가지고 5 분 오른쪽 포크를 기다리고 왼쪽 포크를 일제히두고 5 분 기다리는 상황이 발생한다.
사용할 포크없는 상태가 실제로 컴퓨터 프로그래밍 공유 자원 의 잠금 상태에 대응한다. 자원 잠금은 한 번에 하나의 프로그램 (또는 코드) 만 해당 리소스에 접근하는 것을 보장하는 수단이다. 있는 프로그램이 원하는 자원이 다른 프로그램에 의해 잠겨있는 경우, 그 프로그램은 잠금되는 것을 기다린다. 여러 프로그램이 작동되는 자원과 관련된 경우, 상황에 따라서는 교착 상태가 발생한다. 예를 들어, 프로그램이 처리를하는데 두 파일을 필요로하고 있다고한다. 그런 두 프로그램이 각각 하나 파일을 잠금하는 경우, 두 프로그램 모두 상대가 잠겨있는 파일을 영원히 기다릴 것이다.
식사하는 철학자 문제는 배타 제어 에 관련된 다양한 문제를 설명하기 위해 일반화 추상화 한 것이다. 철학자들이 식사시 경험하는 다양한 장애는 실제로 컴퓨터 프로그래밍에서 공유 리소스에 독점적으로 액세스 할 수있는 경우의 다양한 어려움에 대응하고있다. 이러한 문제는 병행 계산 분야에서 연구되고있다. 다이크 스트라의 원래의 설문은 테이프 드라이브와 같은 외부 주변 장치에 관한 것이었다. 그러나 식사하는 철학자 문제에서 다루어지고있는 것은 여러 프로세스가 일련의 데이터를 업데이트하려고 할 때 발생하는 문제로 일반화 할 수있다. 운영 체제 의 커널 과 같이 다수의 프로세스가 동시에 작동하는 처리 시스템은 수천 개의 잠금 및 동기화 메커니즘을 사용하여 교착 상태 , 자원 부족을 데이터 파괴 등이 일어나지 않도록 그기구의 사용법을 엄격히 지켜야한다.
해법 [ 편집 ]
웨이터를 배치 해법 [ 편집 ]
비교적 간단한 해법은 식탁에 웨이터를 배치하는 것으로한다. 철학자들은 포크를 손에 잡힐 때 반드시 웨이터의 권한을 가지고한다. 웨이터는 어떤 포크를 사용하고 있는지를 파악하고 있기 때문에 교착 상태를 방지 조정 할 수있다. 4 개의 포크가 사용중인 경우, 마지막 포크 철학자가 요구하면 웨이터가 허용을 기다려야 사용중인 포크가 해제 될 때까지 권한은 주어지지 않는다. 철학자가 항상 오른쪽 포크보다 먼저 왼쪽 포크를 잡는 (또는 반대) 같은 결정두면 이야기는 단순화된다. 웨이터는 세마포어 라는 다이크 스트라가 1965 년에 도입 한 개념처럼 행동 [6] .
구체적으로 설명하기 위해 철학자를 시계 방향으로 A에서 E까지 레이블한다. A와 C가 다이어트에서 4 개의 포크를 사용하고 있다고한다. B는 A와 C 사이에 앉아서, 두 포크도 얻을 수없는 반면, D와 E 사이에 사용하지 않는 포크가 1 개 남아있다. 여기서 D가 식사하고 싶다고한다. 그가 다섯 번째 포크를 타고 교착 상태가 발생할 가능성이있다. 그래서 D가 웨이터에게 포크를 매우 좋은 질문, 기다리도록 지시되면, A 또는 C가 식사를 마치고 포크를 놓으면 적어도 1 명의 철학자가 양손에 포크를 가질 수 것이 확실 된다. 따라서 교착 상태가 일어나지 않는다.
자원 계층의 해법 [ 편집 ]
또 간단한 해법은 자원 (이 경우는 포크)에 반 순서 를 할당하는 방법으로 자원의 요구 순서는 항상 자원의 순서대로하여 자원 해제는 그 역순이다.그리고 순서으로 비 관련 리소스를 한 유닛이 동시에 사용할 수는 없다고한다. 자원 (포크)에 1에서 5까지의 번호를 부여하고, 작동 장치 (철학자)는 항상 번호 젊은 분들의 포크를 먼저 취하고, 그 번호의 큰 포크를 취한다. 개별 철학자가 취하는 포크 번호는 정해져있다. 그리고 포크를 넣으면 번호가 큰 분을 먼저두고 그 번호의 젊은 사람의 포크를 둔다. 이 경우, 5 명의 철학자 중 4 명이 동시에 번호의 젊은 사람의 포크를 들면, 번호의 가장 큰 포크 만 남게되고, 5 번째 철학자는 포크를 취할 수 없다. 또한 그 번호가 가장 큰 포크를 취할 철학자는 1 명 밖에 없기 때문에 그 철학자 만 모두 포크를 들고 식사 할 수있다. 그가 식사를 마치고 포크를 놓을 때 먼저 번호 큰에서두고 이어 번호 젊은 분들의 포크를두기 때문에, 후자의 포크를 기다리고 있던 철학자가 포크를 취하고 식사를 시작하는 된다.
이 해법은 다이크 스트라 가 먼저 제안했지만 한개이다.
자원 계층을 사용한 해법은 교착 상태를 막을 수 있지만, 항상 실용적 못하고, 특히 필요한 자원이 처음부터 전부 파악할 수없는 경우에 유용하지 않다. 예를 들어, 운영 단위가 3 번과 5 번 자원을 가지고 있고, 또한 2 번 자원이 필요할 때 자원 획득 순서를 지키기 위해 5 번과 3 번 자원을 일단 해제하지 않으면 2 번 자원을 획득 할 수 없다. 그러고 3 번, 5 번 순서로 획득 다시. 데이터베이스 의 여러 레코드에 액세스하는 컴퓨터 프로그램이있는 경우, 새로운 레코드에 액세스하기 위해 번호의 레코드를 모두 일단 해제해야한다면, 그다지 효율적으로 작동 할 수없는 것이다.
모니터를 사용한 해법 [ 편집 ]
아래의 코드 예제와 해법은 포크가 명시 적으로 나오지 않는다. 철학자는 양쪽 이웃의 철학자가 식사 중이 아닌 경우에만 식사 할 수있다. 즉, 두 번째 포크를 잡히지 않는 철학자는 반드시 포크를 일단두고 기다리고 다시 1 번째에서 시도하는 방식이다.
포크마다 잠금이 없기 때문에 철학자는 양쪽 이웃의 철학자의 상태에 따라 식사를 시작할지 여부를 결정해야하지만, 그 상태 정보가 오래되지 않은 것을 보증 할 필요가있다. 철학자 2 철학자 1이 규정하지 않은 것을 확인한 다음 철학자 3보기 할 때, 1은 2가 3을보고있는 동안 식사를 시작할지도 모른다. 이 해법은 그런 상황을 방지하기 위해 단일 상호 배타 락을 사용한다. 이것은 특정 포크로 이어지는 것이 아니라, 철학자들의 상태를 변경하는 절차 자체에 대응 한 것이다. 그것이 모니터 하는기구이다. 절차 test , pickup , putdown 모니터에 연결되어 있으며, 1 개의 상호 배타적 잠금을 공유한다. 식사 할 수 있도록되기를 기다리는 철학자는 포크가되지 않는다는 점에주의가 필요하다. 식사하고 싶은 철학자가 있으면 모니터는 첫 번째 포크를 놓지하고 두 번째도 입수 가능하게 된 시점에서 1 번째 다시 시도한다. 식사가 끝나면 철학자는 모니터에 신호를 보내 두 포크가 사용 가능한 상태가 된 것을 알게한다.
또한 예로 든 코드는 자원 부족을 막을 수 없다. 예를 들어, 1 번과 3 번 철학자가 식사 시간이 항상 겹쳐 있으면 2 번 철학자는 계속 수용 할 수 없게된다.
스타베숀을 방지하려면 배고픈 철학자가 식사하지 못한 횟수를 유지하고 그것이 한도를 초과하면 철학자 상태 Hungry 에서 Starving 변경한다. 그리고 포크를 부여할지 여부를 판단 할 때 양쪽 이웃이 모두 Starving 아니다라는 조건을 추가 할 필요가있다.
어느 이웃 Starving 였기 때문에 식사 못했다 철학자는 사실상 그 이웃의 이웃이 식사를 끝낼 때까지 기다릴 것이다. 이러한 종속성이 추가 됨으로써 동시성이 줄어든다. Starving 하는 임계 값을 크게하면, 그 영향을 줄일 수있다.
Chandy / Misra의 해법 [ 편집 ]
1984 년 KM Chandy와 J. Misra는 식사하는 철학자 문제에 다른 해법을 제시했다. 그것은 모든 에이전트 (P 1 , ..., P n )이 모든 자원 (R 1 , ..., R m )를 획득하려고하는 상황에 확장 된 것이다. 다이크 스트라의 해법과 달리 순서화도 선택이다. 그들은이 일반화 된 문제를 다음과 같은 해법으로 해결했다.
- 자원을 획득하려고하는 두 철학자의 조합 각각에 대해 포크를 1 개 생성하고 식별 번호 작은 철학자 준다. 이 포크는 dirty 와 clean 의 2 개의 상태가 있고, 초기 상태는 dirty 이다.
- 철학자가 일부 리소스를 함께 사용하려는 경우 (즉, 식사하고 싶은 경우), 충돌하는 이웃 포크을 받아야한다. 그런 자신이 가지고 있지 않은 전 포크에 요청 메시지를 보낸다.
- 요청 메시지를받은 포크를 가진 철학자있는 포크 clean 이라면 가지고 계속하지만, dirty 이라면 그것을 포기. 포크를 요구 한 측에 보낼 때 그것을 clean 상태로 만든다.
- 식사가 끝나자, 포크 dirty 상태가된다. 다른 철학자가 포크를 요구 한 적이 있으면, 그 포크 clean 상태로 보낸다.
이 해법은 대규모 병렬 실행에서도 적용 가능하다.
스타베숀 문제도 해결할 수있다. clean 과 dirty 의 레이블은 가장 오랫동안 식사에 있습니다 붙이지 않은 프로세스를 우선 최근 식사 프로세스의 우선 순위를 낮추는 효과가있다. 철학자가 포크를 놓지 않고 2 회 이상 식사 할 수 없다는 규정을 둔 해법과 비교해 보면, 위에서 언급 한 해법이 더 유연하지만, 경향은 후자와 같다는 것을 알 수있다.
이 분석에서, 그들은 포크 배포 및 clean / dirty 상태로 우선 순위의 시스템을 이끌어 냈다. 그들은이 시스템을 비 환상 그래프로 나타낼지도 모른다 며, 그렇다면, 그 동작은 순환 그래프로 변환 할 수 없게된다. 그것은 교착 상태가 발생하지 않는다는 보장하는 것과 같다. 그러나, 시스템이 먼저 완전히 대칭 상태 (예를 들면, 철학자가 모두 왼쪽 포크를 가지고있는 상태)으로 초기화되는 경우, 그래프는 처음부터 환상이되고 교착 상태를 방지 할 수 없다. 젊은 식별 번호 철학자가 dirty 상태의 포크를 갖게 초기화하면 초기 상태를 비 환상 차트에있다.
해법의 예 [ 편집 ]
다음 코드는 Pascal 로 작성된 해법의 예이다 ( 모니터 를 사용).
PROGRAM d_p ; CONST Doomsday = FALSE ; MONITOR dining_philosophers ; / / 모니터 선언 시작 CONST Eating = 0 ; Hungry = 1 ; Thinking = 2 ; VAR I : INTEGER ; / / 루프 변수 초기화 state : ARRAY [ 0 .. 4 ] OF INTEGER ; / / Eating, Hungry, Thinking can_eat : ARRAY [ 0 .. 4 ] OF CONDITION ; / / 철학자 각각 대응 / / 젓가락이 모인까지 배고픈 철학자를 둔다 PROCEDURE test ( k : INTEGER ) ; BEGIN IF ( state [ k ] = Hungry ) AND ( state [ ( k + 4 ) MOD 5 ] <> Eating ) AND ( state [ ( k + 1 ) MOD 5 ] <> Eating ) THEN BEGIN state [ k ] : = Eating ; SIGNALC ( can_eat [ k ] ) ; / / 대기 상태의 사람이 있으면 그 상태를 종료시키는 END ; END ; PROCEDURE pickup ( i : INTEGER ) ; BEGIN state [ i ] : = Hungry ; WRITELN ( 'philosopher' , i , 'hungry' ) ; test ( i ) ; / / 옆 사람은 식사 중 또는? IF state [ i ] <> Eating THEN WAITC ( can_eat [ i ] ) ; / / 이웃의 식사가 끝날 때까지 기다린다 WRITELN ( 'philosopher' , i , 'eating' ) ; END ; PROCEDURE putdown ( i : INTEGER ) ; BEGIN state [ i ] : = Thinking ; WRITELN ( 'philosopher' , i , 'thinking' ) ; test ( ( i + 4 ) MOD 5 ) ; / / 왼쪽 이웃이 식사하는 기회 을주는 test ( ( i + 1 ) MOD 5 ) ; / / 오른쪽 이웃이 식사하는 기회를 준다 END ; BEGIN / / 모니터를 초기화 FOR I : = 0 TO 4 DO state [ i ] : = Thinking ; END ; / / 모니터 정의의 끝 PROCEDURE philosopher ( i : INTEGER ) ; BEGIN REPEAT pickup ( i ) ; / / 젓가락을 잡는 putdown ( i ) ; / / 젓가락을 두는 UNTIL Doomsday ; END ; BEGIN / / 주 프로그램 COBEGIN / / 5 개의 프로세스를 동시에 시작 philosopher ( 0 ) ; philosopher ( 1 ) ; philosopher ( 2 ) ; philosopher ( 3 ) ; philosopher ( 4 ) ; COEND ; END
다음 코드는 Java로 작성된 해법의 예이다 ( 세마포어 를 사용).
import java.util.concurrent.Semaphore ; import java.util.Random ; import java.util.Vector ; public class philosopher extends Thread { private static Final Random rand = New Random ( ) ; private static int event = 0 ; private static String binary = "" ; private int ID ; private Semaphore SEM ; private static Vector < Object [ ] > vector = New Vector < Object [ ] > ( ) ; public philosopher ( int I, Semaphore s ) { id = i ; sem = s ; binary = binary + "0" ; } private void busy ( ) { try { sleep ( rand. nextInt ( 1000 ) ) ; } catch ( InterruptedException e ) { } } private void thinking ( ) { String str = "Philosopher" + id + "is thinking" ; vector. add ( this . addToObject ( System . currentTimeMillis ( ) , event, str ) ) ; event + +; busy ( ) ; } private void eating ( ) { String str = "Philosopher" + id + "is hungry and is trying to pick up his chopsticks" ; vector. add ( this . addToObject ( System . currentTimeMillis ( ) , event, str ) ) ; event + +; busy ( ) ; str = "Philosopher" + id + "is eating" ; this . oneToBinary ( id ) ; vector. add ( this . addToObject ( System . currentTimeMillis ( ) , event, str ) ) ; event + +; busy ( ) ; str = "Philosopher" + id + "finished eating, and puts away his chopsticks" ; this . zeroToBinary ( id ) ; vector. add ( this . addToObject ( System . currentTimeMillis ( ) , event, str ) ) ; event + +; } private Object [ ] addToObject ( long T, int I, String s ) { Object [ ] o = New Object [ 4 ] ; o [ 3 ] = s ; o [ 2 ] = i ; o [ 1 ] = binary ; o [ 0 ] = t ; return O ; } private void oneToBinary ( int I ) { binary = binary. substring ( 0 , i ) + "1" + binary. substring ( i + 1 ) ; } private void zeroToBinary ( int I ) { binary = binary. substring ( 0 , i ) + "0" + binary. substring ( i + 1 ) ; } @ Override public void run ( ) { for ( int I = 0 ; i < 10 ; + + i ) { thinking ( ) ; try { sem. acquire ( ) ; } catch ( InterruptedException e ) { } eating ( ) ; sem. release ( ) ; } } public static void Main ( String [ ] args ) { Final int N = 5 ; Semaphore sem = New Semaphore ( N, true ) ; Philosopher [ ] philosopher = New philosopher [ N ] ; / / 철학자를 생성 for ( int I = 0 ; i < N ; i + + ) { philosopher [ i ] = New philosopher ( i, sem ) ; philosopher [ i ] . start ( ) ; } / / 완료待ち合わせる for ( int I = 0 ; i < N ; i + + ) { try { philosopher [ i ] . join ( ) ; } catch ( InterruptedException EX ) { return ; } } for ( int I = 0 ; i < vector. size ( ) ; i + + ) { Object [ ] o = vector. get ( i ) ; System . out . printf ( "% d % d % s % s \ n " , o [ 0 ] , o [ 2 ] , o [ 1 ] , o [ 3 ] ) ; } } }
각주 [ 편집 ]
- ^ Dijkstra, Edsger W. EWD-1000. EW Dijkstra Archive. Center for American History, University of Texas at Austin. ( original ; transcription )
- ^ J. Díaz; I. Ramos (1981). Formalization of Programming Concepts : International Colloquium, Peniscola, Spain, April 19-25, 1981. Proceedings . Birkhäuser. pp. 323 , 326 . ISBN 978-3-540-10699 - 9 .
- ^ Hoare, CAR ( 2004 년 ). " Communicating Sequential Processes " . usingcsp.com (originally published in 1985 by Prentice Hall International) 2012 년 7 월 16 일 보기.
- ^ 해외에서 예
- ^ Dijkstra, Edsger W. EWD-310. EW Dijkstra Archive. Center for American History, University of Texas at Austin. ( original ; transcription )
- ^ Dijkstra, Edsger W. EWD-123. EW Dijkstra Archive. Center for American History, University of Texas at Austin. ( original ; transcription )
참고 문헌 [ 편집 ]
- Silberschatz, Abraham; Peterson, James L. (1988). Operating Systems Concepts . Addison-Wesley. ISBN 0-201-18760-4 .
- Chandy, KM; Misra, J. (1984). The Drinking Philosophers Problem . ACM Transactions on Programming Languages and Systems.
- Dijkstra, EW (1971, June). Hierarchical ordering of sequential processes . Acta Informatica 1 (2) : 115-138.
- Lehmann, DJ, Rabin M. O (1981) On the Advantages of Free Choice : A Symmetric and Fully Distributed Solution to the Dining Philosophers Problem. Principles Of Programming Languages 1981 ( POPL '81), pp. 133-138.
관련 항목 [ 편집 ]
- Drinking philosophers problem
- 졸고 이발소 문제
- en : Cigarette smokers problem
- 식사하는 암호 학자의 문제 이름은 비슷하지만 문제 관련은 없다.
외부 링크 [ 편집 ]
- 식사하는 철학자 문제 (Java 애플릿) (영어) (프랑스어) (독일어)
- 식사하는 철학자
- 철학자들의 식사
- ObjectClub - diningPhilosopher
- Discussion of the problem with solution code for 2 or 4 philosophers
- Discussion of various solutions 1
- Discussion of various solutions 2
- Discussion of a solution using continuation based threads (cbthreads)
- Distributed symmetric solutions
- Programming the Dining Philosophers with Simulation
- interactive example of the Philosophers problem (Java 애플릿)
- Satan Comes to Dinner
- Wot No Chickens?
- ThreadMentor
- Solving The Dining Philosophers Problem With Asynchronous Agents
- Rosetta Code : Dining philosophers - 다양한 언어로 구현 예
식사하는 철학자들 문제는 전산학에서 동시성과 교착 상태를 설명하는 예시로, 여러 프로세스가 동시에 돌아갈 때 교착 상태가 나타나는 원인을 직관적으로 알 수 있다.
다섯 명의 철학자가 원탁에 앉아 있고, 각자의 앞에는 스파게티가 있고 양옆에 젓가락이 하나씩이 있다. 그리고 각각의 철학자는 다른 철학자에게 말을 할 수 없다. 이때 철학자가 스파게티를 먹기 위해서는 양 옆의 젓가락을 동시에 들고 있어야 한다. 이때 각각의 철학자가 왼쪽의 젓가락을 들고 그 다음 오른쪽의 젓가락을 들어서 스파게티를 먹는 알고리즘을 가지고 있으면, 다섯 철학자가 동시에 왼쪽의 젓가락을 든 다음 오른쪽의 젓가락을 들 때까지 무한정 기다리는 교착 상태에 빠지게 될 수 있다.
또한 어떤 경우에는 동시에 두 젓가락을 집을 수 없어 식사를 하지 못하는 기아 상태가 발생할 수도 있고, 몇몇 철학자가 다른 철학자보다 식사를 적게 하는 경우가 발생하기도 한다.
[편집]해결책
에츠허르 데이크스트라의 해결책은 다음과 같다. 각각의 철학자를  라고 하고, 각 철학자의 왼쪽 젓가락을
라고 하고, 각 철학자의 왼쪽 젓가락을  라고 하자.
라고 하자.  를 제외한 네 명은 먼저
를 제외한 네 명은 먼저 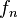 를 집은 후
를 집은 후  를 집는 방식을 취한다. 그리고
를 집는 방식을 취한다. 그리고  는 이와 반대로,
는 이와 반대로, 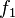 를 먼저 집은 후
를 먼저 집은 후  를 집는다. 이것은 원래 방식의 대칭성을 제거하고, 따라서 교착 상태를 막을 수 있다.
를 집는다. 이것은 원래 방식의 대칭성을 제거하고, 따라서 교착 상태를 막을 수 있다.
[편집]같이 보기
[편집]바깥 고리
- (영어/프랑스어/독일어) 식사하는 철학자들 문제 (자바 애플릿)
- 철학자들의 만찬 문제
'System > Common' 카테고리의 다른 글
| 경영 정보학(Business Intelligence, BI) (0) | 2012.10.27 |
|---|---|
| Lustre 파일시스템이란? (0) | 2012.10.27 |
| awk (0) | 2012.08.30 |
| UNIX 시스템에 필요한 10가지 핵심 도구 (0) | 2012.08.23 |
| 캐리지 리턴(CR)과 라인 피드(LF), 뉴라인(/n) (0) | 2012.08.11 |






